Floating Point Numbers in Binary

Floating point is a method of storing a wide range of real numbers (numbers with a decimal point) in binary.

You may be familiar with scientific notation:

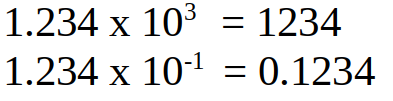
It’s usually used for numbers that are very large or very small where they become impractical to write down.

To work out what number is meant, we multiply 1.234 (the mantissa) by 10 (the base) raised to the stated power (the exponent). In the first example we multiply 1.234 by 10 cubed (1000) which gives us 1234. In the second example we multiply 1.234 by 10 raised to to power of -1, which is 0.1, and this gives us 0.1234.

The floating point method of representing numbers in binary works in the same way. We have a mantissa and an exponent. The only difference is the exponent has a base of 2 (because it’s binary) instead of 10 for decimal.

There are many different ways these kinds of numbers can be stored, however one popular standard for floating point that is used in most computers uses 32 bits (4 bytes) to represent each number. This method is known by the catchy name IEEE 754. The format looks like this:

• The left hand bit is used to represent the sign of the number (plus or minus)
• The next 8 bits are used to represent the exponent part of the number as a power of 2
• The remaining 23 bits are used to store the mantissa

The sign bit is very simple. It is 0 for positive numbers and 1 for negative numbers.

The left-most bit of the mantissa represents 1/2. The 2nd bit from the left represents 1/4 and then the 3rd bit represents an 1/8th and so on. Each successive bit as you move further right is worth half of the previous one. This is just like in decimal where after the decimal point each successive digit position as you move to the right is worth 1/10 as much as the previous digit because the counting system is based on 10s. In binary the counting system is based on 2s, so each successive digit position as you move to the right divides by 2 instead.

There’s actually an “invisible” bit at the start of the mantissa which represents the number 1. Every mantissa in IEEE 754 starts with a 1 and so this bit is missed out to save space as it would always be set to 1 regardless.

For completeness is should be said there is technically one exception where there is not a leading 1 but it is very rarely used (see denormalised numbers below). For most practical purposes assume the leading 1 is always present.

The exponent is stored with 127 added to it. So for example, an exponent of 1 is stored at 127 + 1 = 128. An exponent of 2 is stored as 127 + 2 = 129 and so on. An exponent of -1 is 127 + -1 = 126. Remember that the exponent is a power of 2.

Examples

The number 3 is stored as:

1.5 x 2^1 = 3

Two raised to the power of 1 is just 2. So this means 1.5 x 2 = 3. Here’s how it looks in binary in IEEE 754 format:

• The mantissa bit for 1/2 is set (the left-most one). There is an assumed 1 that is invisible, so in total we have 1.5 in the mantissa.
• The exponent is set to 1. The exponent always has 127 added to it so the binary number 128 is actually stored in the usual binary fashion. As the exponent is 8 bits, that means the left-most bit is set to 1 to mean 128 and all the other bits are zero.
• The sign bit is set to zero because 3 is a positive number and zero means positive

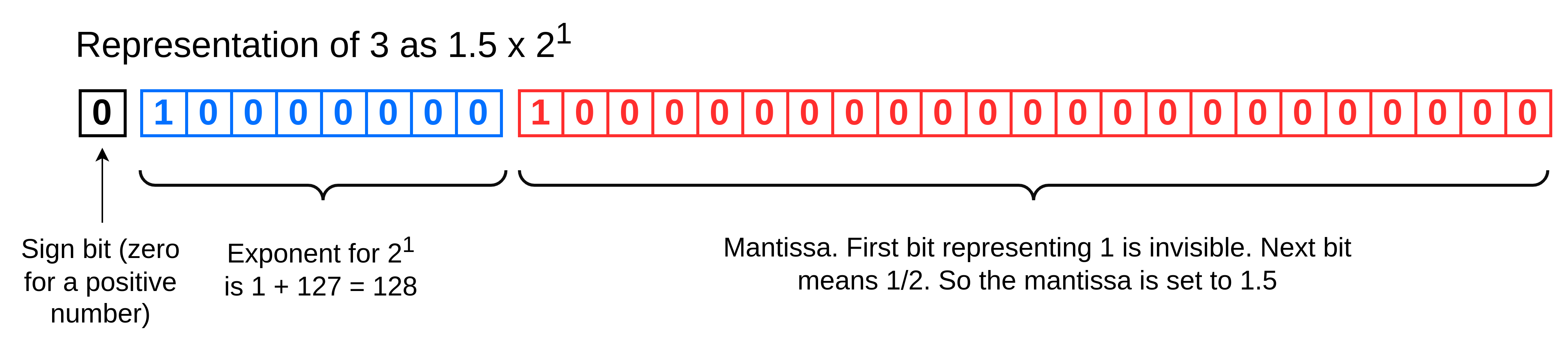
Now let’s look at the number -0.4375. This is stored as:

-1.75 x 2^-2 = -0.4375

• The mantissa has the bits for 1/2 and 1/4 set. Then there is the assumed 1. So the mantissa is set to 1 + 0.5 + 0.25 = 1.75.
• The exponent is -2, so this is stored with 127 added to it = 125
• Then we have the sign bit set set to 1 because it’s a negative number

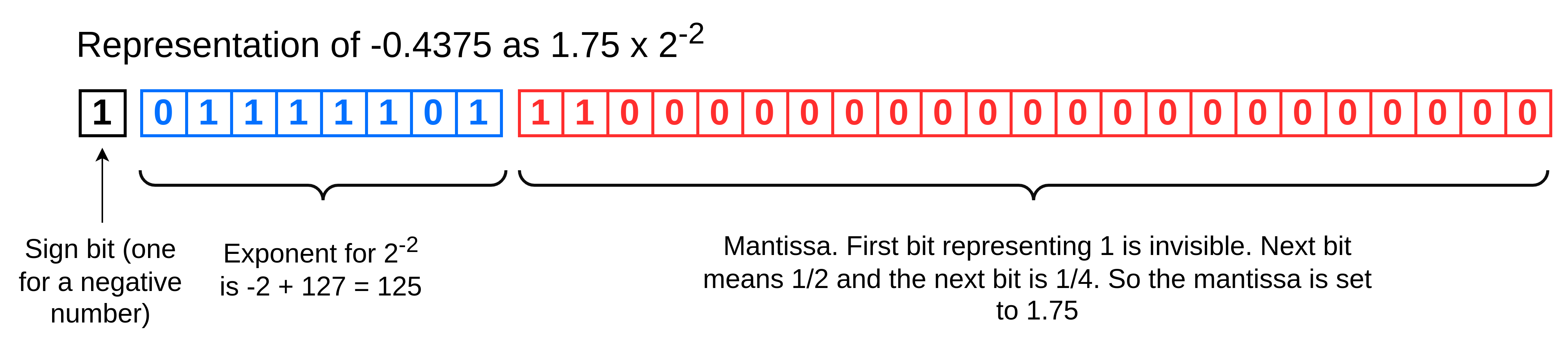
So how would we figure out what the mantissa and exponent is for any particular number? For practical purposes you’re unlikely to ever need to do the conversion yourself as all programming languages will convert decimal into floating point and back for you automatically as standard. If you are interested to find out though, this article explains how to convert decimal numbers into IEEE 754 floating point.

Accuracy Problems with Floating Point Numbers

Python uses IEEE 754 by default to represent real numbers. Let’s add 0.1 to 0.2 and then check that it equals 0.3, which of course we expect that it should.

>>> a = 0.1
>>> b = 0.2
>>> c = 0.3
>>> a + b == c
False

Huh? Python says False. It thinks 0.1 + 0.2 does not equal 0.3. Why does that happen?

The problem is that not all floating point numbers can be accurately represented in IEEE 754. Let’s take a closer look at the numbers with more decimal places visible:

>>> a = 0.1
>>> b = 0.2
>>> c = 0.3

>>> format(a, '.20f')
'0.10000000000000000555'
>>> format(b, '.20f')
'0.20000000000000001110'
>>> format(c, '.20f')
'0.29999999999999998890'

Now we can see the problem. When we look at the numbers with 20 decimal places, we see that Python thinks the ‘a’ variable, which should be 0.1, is actually 0.10000000000000000555. It thinks ‘b’ is 0.20000000000000001110 instead of 0.2 and ‘c’ is 0.29999999999999998890 where it should be 0.3.

So indeed, if you add a and b it does not equal c at all.

But why didn’t Python put exactly 0.1 into the ‘a’ variable like we asked for? The answer is it can’t. There’s actually no way to represent precisely 0.1 in this floating point system. You can only get a number very close to 0.1, so Python gives us the nearest number that it can.

The advantage of IEEE 754 floating point numbers is we can represent a very wide range of numbers. However the disadvantage is they are slightly inaccurate. This makes floating point unsuitable for some kinds of software e.g. we try and avoid using floating point in financial calculations because people get annoyed when the pennies in their bank accounts don’t add up! As a rule of thumb, never use a floating point number when an integer will do.

Alternative Precision

There is another standard in IEEE 754 which uses 64-bits instead of 32-bits. It is largely the same as the 32-bit version except it uses 11 bits for the exponent, 52 bits for the mantissa and with the sign bit that’s 64 bits. In programming the 32-bit version is often referred to as single precision and the 64-bit standard as double precision. Support for both of these is widespread in most programming languages and hardware. Python uses the 64-bit version by default. Using 64-bits doesn’t make floating point completely accurate, but it does make it more accurate than using 32-bits.

There is also quadruple precision (128-bits) and even octuple precision (256-bits) but they are more rarely used than double precision which is often sufficient for many applications. At the time of writing hardware support for 128-bit can sometimes be found but octuple precision is unusual.

There has been interest in making smaller versions of IEEE 754 floating point numbers in 16 bits and less. The 16-bit version is called half precision. Smaller versions are less accurate so why would anyone want that? One reason is that artificial intelligence requires a lot of floating point numbers and it has been discovered that less accurate versions are good enough. The fewer bits that are used for each number then the less memory is required to store them and the cheaper the AI system can be.

Fixed point arithmetic is another alternative to floating point as is BCD (Binary Coded Decimal).

There are software libraries that can work with numbers in more like the way people do and produce accurate results. For example the Python “decimal” module gives the right answer where IEEE 754 doesn’t work:

>>> from decimal import *
>>> a = Decimal('0.1')
>>> b = Decimal('0.2')
>>> c = Decimal('0.3')
>>> a+b == c
True

Why would you not want to use this software library if it produces more accurate results? The reason is speed. Almost all modern computers have specialised circuitry for handling IEEE 754 numbers and these numbers can be processed very considerably faster.

Special Cases and Exceptions

There are a few special cases in IEEE 754 floating point numbers:

• Zero is represented when the exponent and mantissa are both zero but the sign bit can be either 0 or 1. So there are two zeros in the standard.
• Infinity is supported and is represented when the exponent has all bits set and the mantissa is zero. The sign bit signifies negative or positive infinity.
• There is NaN which means “not a number” which programmers quite often see. This means there is an error. Some languages will return NaN when performing operations such as the square root of minus 1, division by zero or nonsensical conversions such as trying to convert text into a number. Occasionally NaN is used as a marker when a number is missing. NaN is signified by the exponent with all bits set and the mantissa is not zero.
• Denormalised numbers are a special and rarely used case supported by IEEE 754 for very small numbers that are close to but not exactly zero. When the exponent is all zeros and the mantissa is not zero there is a denormalised number. In this mode the mantissa does not have an assumed 1 at the beginning. The numbers are otherwise interpreted as above.